目录
快速导航-
卷首语 | 走近杨乐
卷首语 | 走近杨乐
-
数学之基 | 从朱建华跳过2.38米说起
数学之基 | 从朱建华跳过2.38米说起
-
数学之基 | 经历抽象过程 发展推理能力
数学之基 | 经历抽象过程 发展推理能力
-

数学之基 | “代数式”与“整式的加减”
数学之基 | “代数式”与“整式的加减”
-
数学之基 | 在运动中掌握知识
数学之基 | 在运动中掌握知识
-
数学之基 | 感悟符号本质 发展代数意识
数学之基 | 感悟符号本质 发展代数意识
-
数学之基 | 掌握概念 提高能力
数学之基 | 掌握概念 提高能力
-

数学之基 | 小心“陷阱”
数学之基 | 小心“陷阱”
-

数学之基 | 多角度剖析 全方位认识
数学之基 | 多角度剖析 全方位认识
-
数学之基 | 厘清概念 明确算理
数学之基 | 厘清概念 明确算理
-

数学之趣 | 笑笑漫游数学世界之单项式的系数
数学之趣 | 笑笑漫游数学世界之单项式的系数
-

数学之趣 | 两道拼图趣题
数学之趣 | 两道拼图趣题
-
数学之趣 | 东东“闯关”记
数学之趣 | 东东“闯关”记
-
数学之趣 | 积极应对学习成绩下降引发的心理焦虑
数学之趣 | 积极应对学习成绩下降引发的心理焦虑
-
数学之趣 | 数学创新思维竞赛
数学之趣 | 数学创新思维竞赛
-
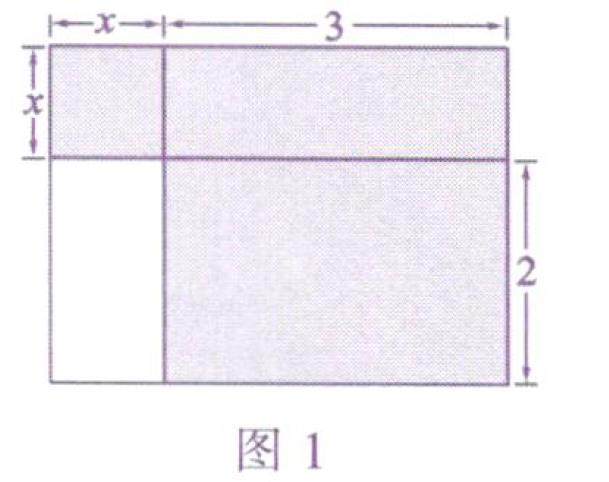
数学之用 | “列代数式表示数量关系”基础夯实
数学之用 | “列代数式表示数量关系”基础夯实
-
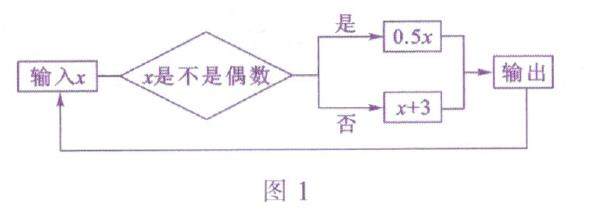
数学之用 | “代数式的值”要点攻克
数学之用 | “代数式的值”要点攻克
-

数学之用 | “整式”巩固进阶
数学之用 | “整式”巩固进阶
-

数学之用 | “整式的加法与减法”核心通关
数学之用 | “整式的加法与减法”核心通关
-

数学之用 | “整式的加减”易错点诊断
数学之用 | “整式的加减”易错点诊断
-

数学之用 | 参考答案
数学之用 | 参考答案























 登录
登录