目录
快速导航-
刊首语 | 斜学与传媒
刊首语 | 斜学与传媒
-

引探导航 | “曲线运动”重难点分析与学法指导
引探导航 | “曲线运动”重难点分析与学法指导
-

引探导航 | 小船渡河问题的解读与拓展
引探导航 | 小船渡河问题的解读与拓展
-

引探导航 | 化解“运动的合成与分解”学习难点
引探导航 | 化解“运动的合成与分解”学习难点
-

引探导航 | 伽利略变换在相对运动中的应用
引探导航 | 伽利略变换在相对运动中的应用
-

引探导航 | 假设思维在曲线运动中的运用
引探导航 | 假设思维在曲线运动中的运用
-

引探导航 | 研究抛体运动的分解方法
引探导航 | 研究抛体运动的分解方法
-
引探导航 | 世界著名的物理实验室(二)
引探导航 | 世界著名的物理实验室(二)
-

引探导航 | 速度的分解及运用
引探导航 | 速度的分解及运用
-

题中悟道 | 当平抛遇到斜面
题中悟道 | 当平抛遇到斜面
-

题中悟道 | 几个典型的水平面内圆周运动临界问题分析
题中悟道 | 几个典型的水平面内圆周运动临界问题分析
-

题中悟道 | 竖直平面内圆周运动的临界问题
题中悟道 | 竖直平面内圆周运动的临界问题
-
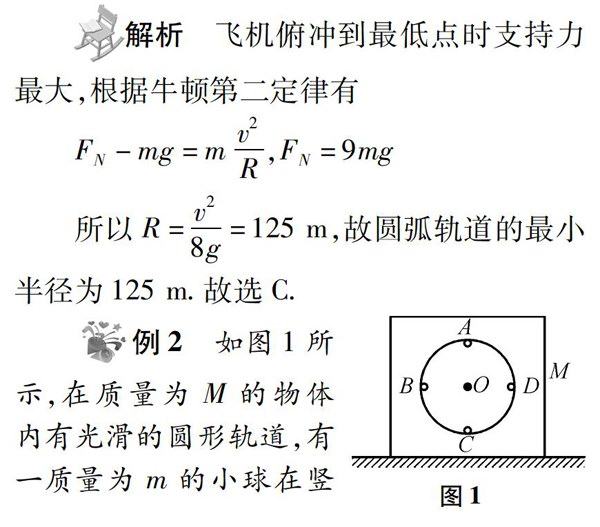
题中悟道 | 竖直平面内圆周运动实例分析
题中悟道 | 竖直平面内圆周运动实例分析
-
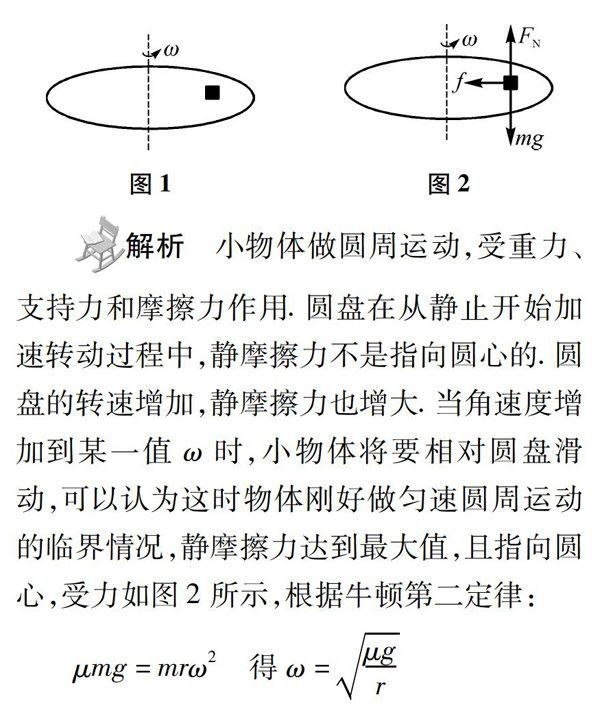
题中悟道 | 水平面内圆周运动实例分析
题中悟道 | 水平面内圆周运动实例分析
-
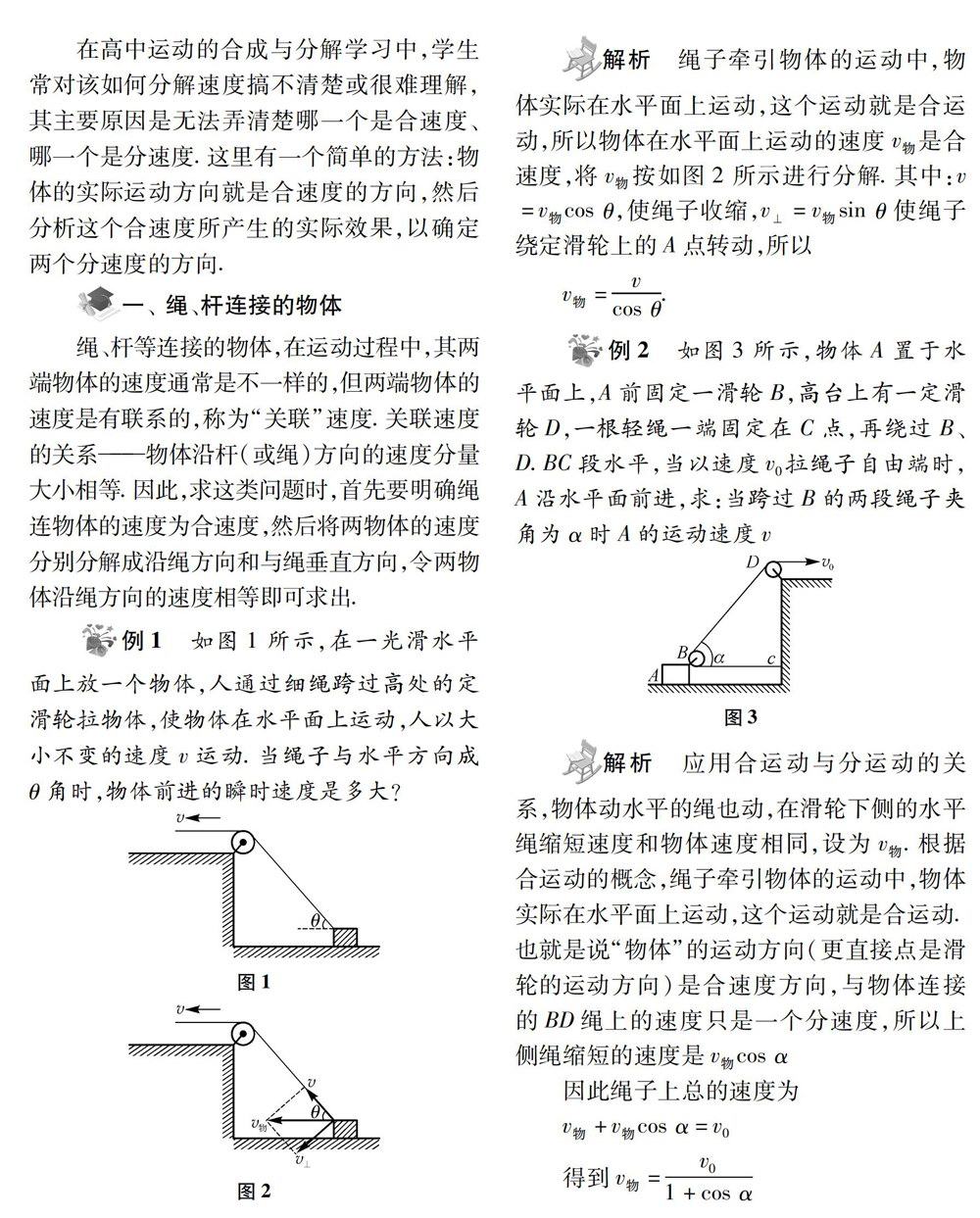
题中悟道 | 速度关联类问题求解
题中悟道 | 速度关联类问题求解
-

题中悟道 | 圆周运动的多解性问题
题中悟道 | 圆周运动的多解性问题
-
题中悟道 | “曲线运动”测试卷A
题中悟道 | “曲线运动”测试卷A
-

题中悟道 | “曲线运动”测试卷B
题中悟道 | “曲线运动”测试卷B
-

题中悟道 | 小船渡河问题赏析
题中悟道 | 小船渡河问题赏析
-

学以致用 | 风从哪里来,雨往哪里去?
学以致用 | 风从哪里来,雨往哪里去?
-

学以致用 | 生活中国周运动典型问题
学以致用 | 生活中国周运动典型问题
-

学以致用 | 斜上抛运动的最大射程问题刍议
学以致用 | 斜上抛运动的最大射程问题刍议
-
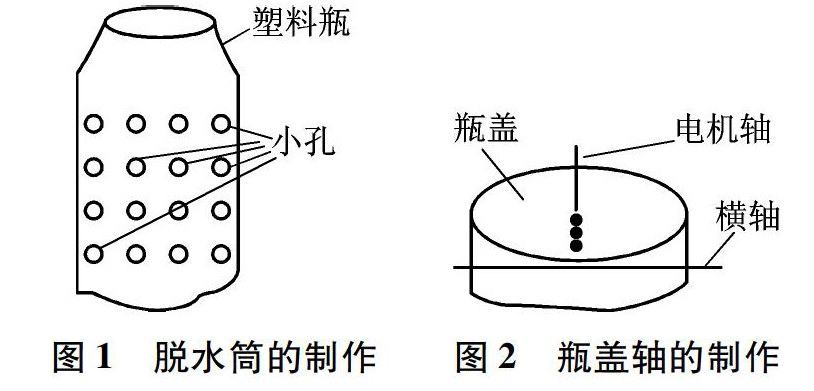
学以致用 | 自制洗衣机脱水原理演示器
学以致用 | 自制洗衣机脱水原理演示器
-

学以致用 | 空气阻力对斜抛运动的影响
学以致用 | 空气阻力对斜抛运动的影响
-
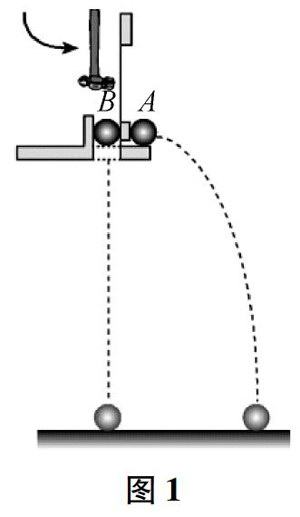
实验天地 | 关于平抛运动的常见验证性实验
实验天地 | 关于平抛运动的常见验证性实验
-
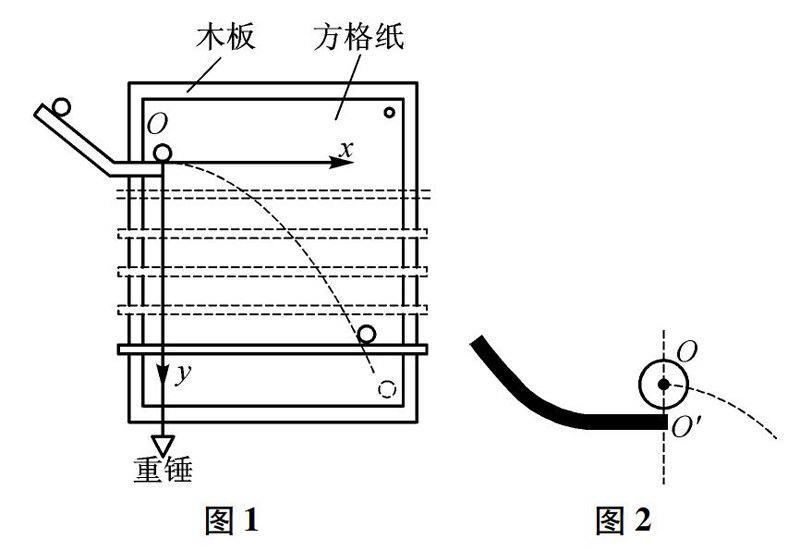
实验天地 | 探究平抛运动轨迹
实验天地 | 探究平抛运动轨迹



















 登录
登录