目录
快速导航-
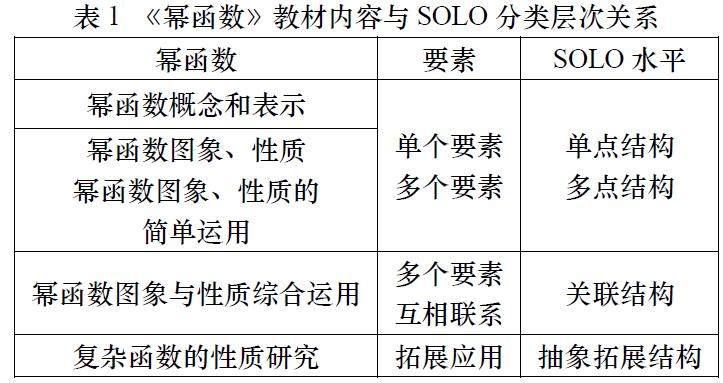
数学教育 | SOLO分类理论在高中数学“5G+专递课堂”教学的应用
数学教育 | SOLO分类理论在高中数学“5G+专递课堂”教学的应用
-
数学教育 | 聚焦“数学美” 渗透五育融合
数学教育 | 聚焦“数学美” 渗透五育融合
-
数学教育 | 深度学习理念下高中生数学思维能力培养的路径探究
数学教育 | 深度学习理念下高中生数学思维能力培养的路径探究
-

数学教育 | 基于情理美教学主张的数学教学实践探究
数学教育 | 基于情理美教学主张的数学教学实践探究
-
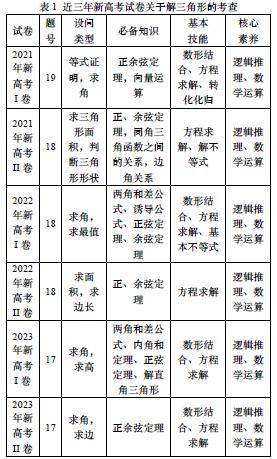
教学研究 | 指向深度学习的高三复习课的实践与反思
教学研究 | 指向深度学习的高三复习课的实践与反思
-
教学研究 | 一图一专题:二次函数专题复习走向纵深的尝试
教学研究 | 一图一专题:二次函数专题复习走向纵深的尝试
-

教学研究 | 寻思考路径 促思维进阶
教学研究 | 寻思考路径 促思维进阶
-
教学研究 | 浅谈一元一次含参方程的教学策略
教学研究 | 浅谈一元一次含参方程的教学策略
-

教学研究 | 运用变式教学法改进试卷讲评课的实践路径
教学研究 | 运用变式教学法改进试卷讲评课的实践路径
-
教学研究 | 两节同课异构课的对比及反思
教学研究 | 两节同课异构课的对比及反思
-
试题研究 | 问题为导 思维为先 素养为核
试题研究 | 问题为导 思维为先 素养为核
-

试题研究 | 一道教材习题改编成参赛压轴题的命制过程及感悟
试题研究 | 一道教材习题改编成参赛压轴题的命制过程及感悟
-

试题研究 | 深入理解 注重联系 提升素养
试题研究 | 深入理解 注重联系 提升素养
-

试题研究 | 引而伸之 触类而长之
试题研究 | 引而伸之 触类而长之
-

数学建模 | 学校食堂选餐中的数学问题
数学建模 | 学校食堂选餐中的数学问题
-
信息技术 | 高中数学人教A版教材算例的MATLAB对比实践
信息技术 | 高中数学人教A版教材算例的MATLAB对比实践






















 登录
登录