目录
快速导航-

特稿 | 论代数运算的基本原理及其思维进阶模式
特稿 | 论代数运算的基本原理及其思维进阶模式
-
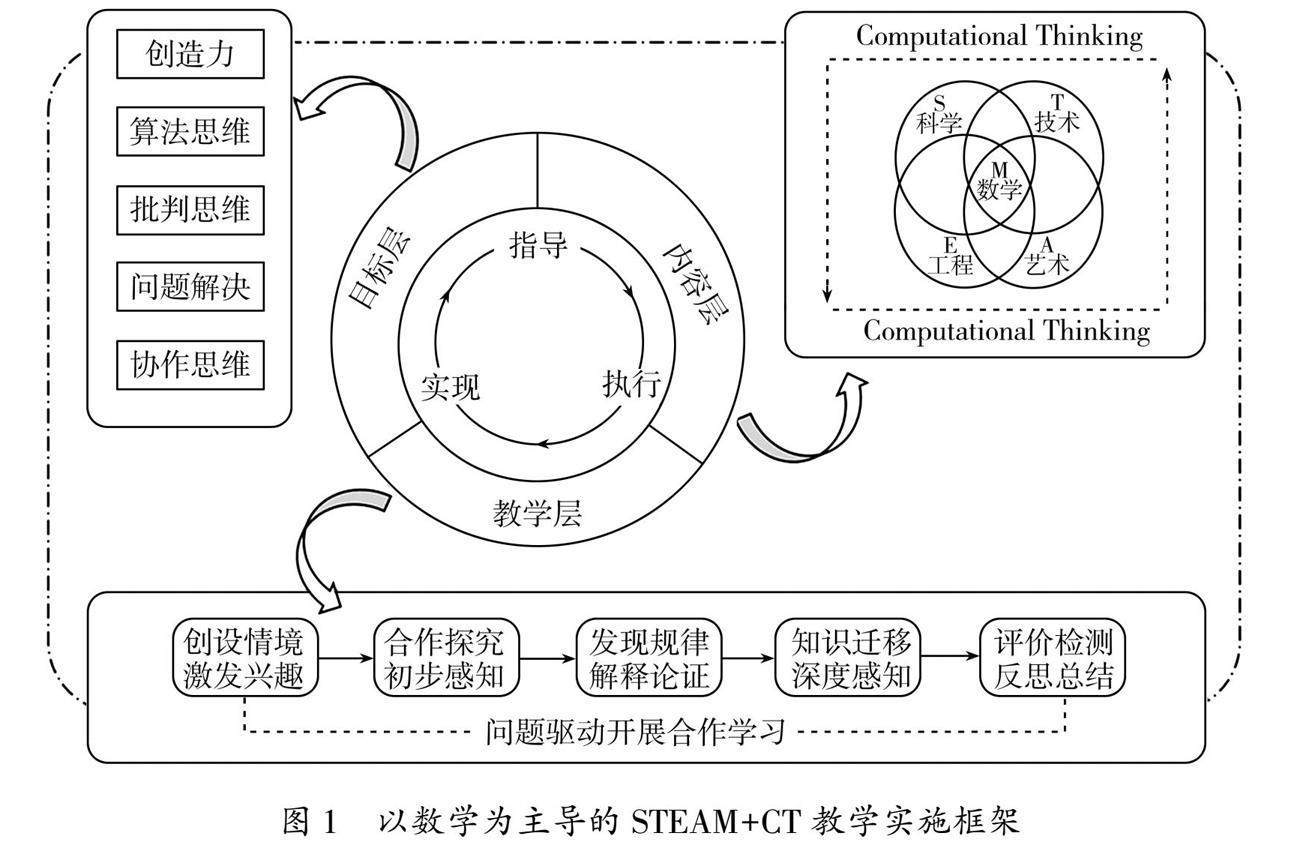
数学教育 | 以数学为主导的多学科融合教学促进计算思维培养:实施框架与课例开发
数学教育 | 以数学为主导的多学科融合教学促进计算思维培养:实施框架与课例开发
-

教学研究 | 信息技术助力数学建模素养的发展
教学研究 | 信息技术助力数学建模素养的发展
-

教学研究 | 例说确定数学教学“序”的多样化路径
教学研究 | 例说确定数学教学“序”的多样化路径
-
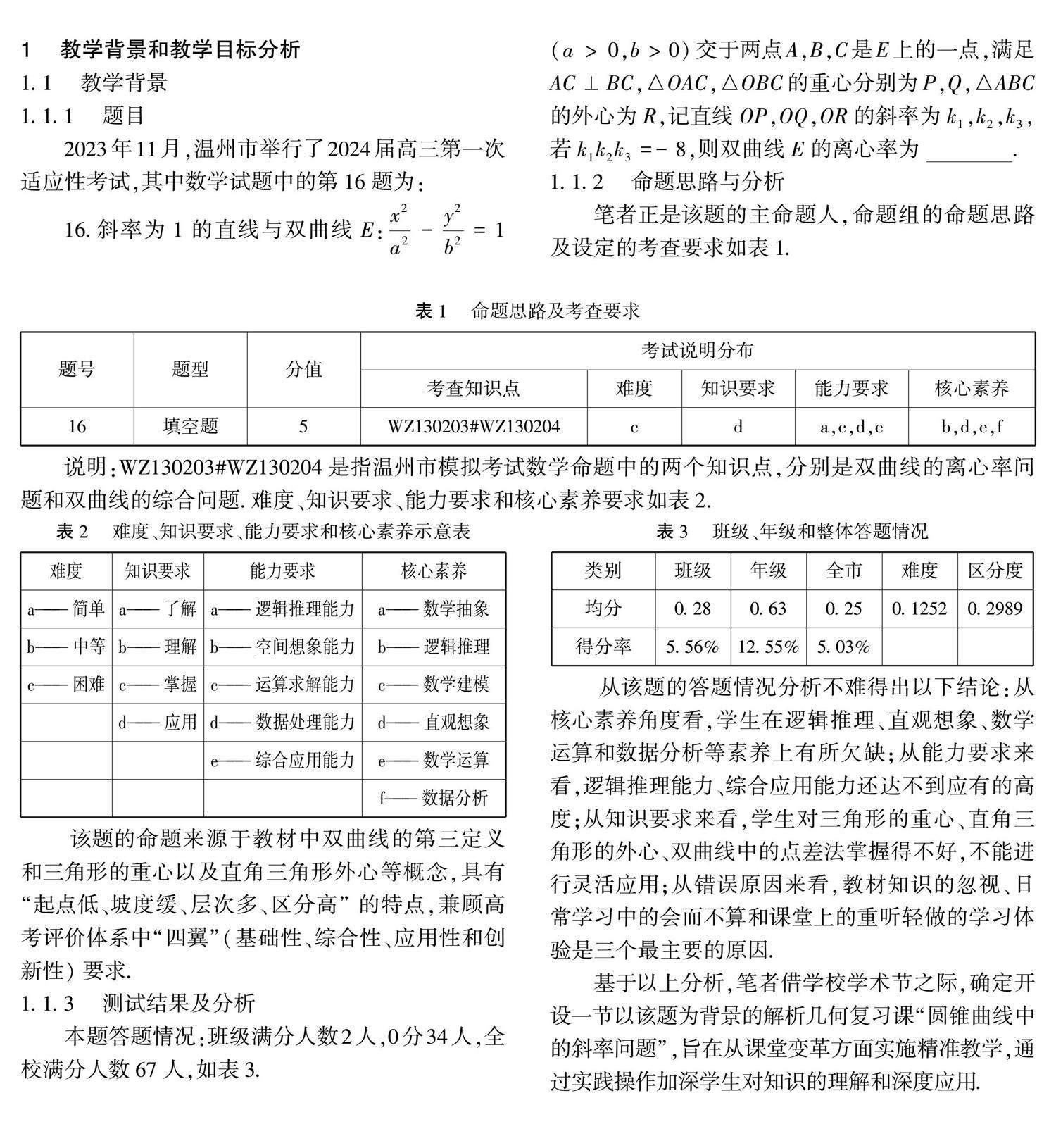
教学研究 | 精研判堵点 深度做中学
教学研究 | 精研判堵点 深度做中学
-
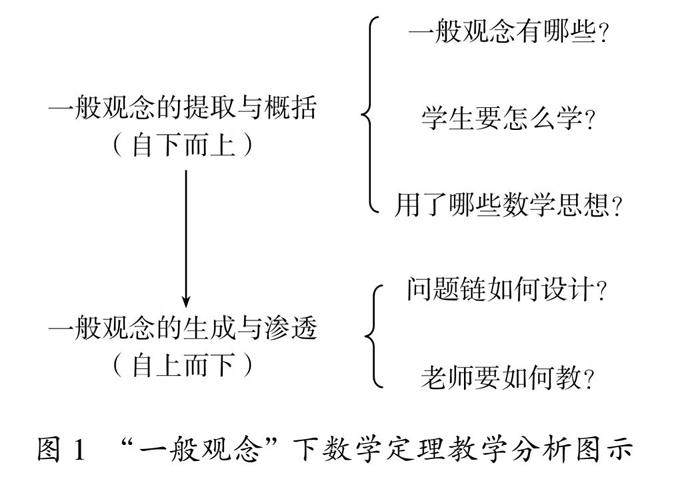
教学研究 | “一般观念”引领下的数学定理教学设计
教学研究 | “一般观念”引领下的数学定理教学设计
-
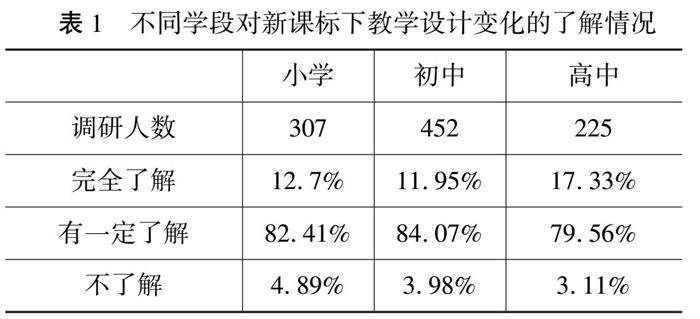
教师发展 | 核心素养下数学教师教学行为的转变与成效分析
教师发展 | 核心素养下数学教师教学行为的转变与成效分析
-
教师发展 | 青年数学教师专业成长的六大抓手
教师发展 | 青年数学教师专业成长的六大抓手
-

思路与方法 | 建构问题链 实现思维进阶
思路与方法 | 建构问题链 实现思维进阶
-

思路与方法 | 深挖教材习题 提升备考效率
思路与方法 | 深挖教材习题 提升备考效率
-

高考试题研究 | 融五育为树人 考思维促选才 重教材引教学
高考试题研究 | 融五育为树人 考思维促选才 重教材引教学
-

高考试题研究 | 多措并举拓宽视野 背景探究体现本质
高考试题研究 | 多措并举拓宽视野 背景探究体现本质
-

高考试题研究 | 2024年全国新课标Ⅰ卷第17题解析与教学启示
高考试题研究 | 2024年全国新课标Ⅰ卷第17题解析与教学启示
-

高考试题研究 | 考查数学思维和综合能力 选拔国家需要的数学人才
高考试题研究 | 考查数学思维和综合能力 选拔国家需要的数学人才
-

高考试题研究 | 高考数学“新定义型”压轴题的命制研究
高考试题研究 | 高考数学“新定义型”压轴题的命制研究
















 登录
登录