目录
快速导航-

课程教材教法 | 探源析流,启思践行2024年盐城中考数学第27题深度解析与教学启示
课程教材教法 | 探源析流,启思践行2024年盐城中考数学第27题深度解析与教学启示
-
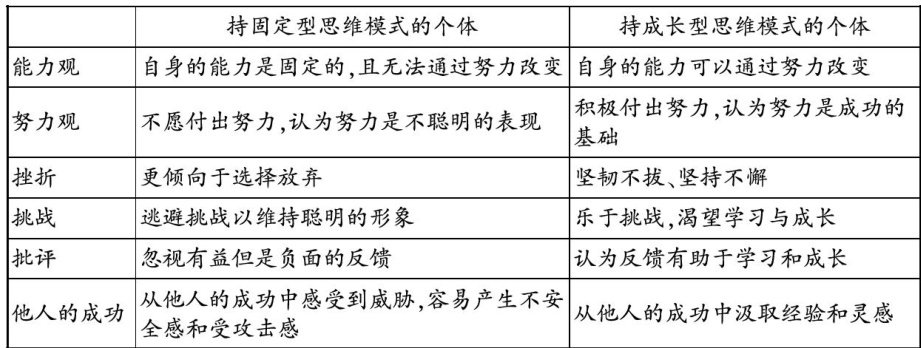
课程教材教法 | 数学挑战性任务和成长型思维培养: 内在关联与初中教学策略
课程教材教法 | 数学挑战性任务和成长型思维培养: 内在关联与初中教学策略
-
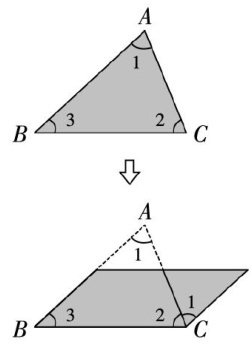
课程教材教法 | 让几何定理的学习经验在探索活动中自然生成
课程教材教法 | 让几何定理的学习经验在探索活动中自然生成
-

课例评析 | 智教·智学·智评智慧课堂背景下初中数学教一学一评”一体化教学设计微探
课例评析 | 智教·智学·智评智慧课堂背景下初中数学教一学一评”一体化教学设计微探
-

课例评析 | 依托历史文化素材 培养数学阅读能力
课例评析 | 依托历史文化素材 培养数学阅读能力
-

课例评析 | 基于“生本"理念的数学教学实践与研究
课例评析 | 基于“生本"理念的数学教学实践与研究
-

课例评析 | 立足章起始课教学 发展数学核心素养
课例评析 | 立足章起始课教学 发展数学核心素养
-
教学实践 | 促进深度学习的初中数学跨学科主题学习
教学实践 | 促进深度学习的初中数学跨学科主题学习
-

教学实践 | 单元整体视域下基于思维发展的数学教学实践与研究
教学实践 | 单元整体视域下基于思维发展的数学教学实践与研究
-

教学实践 | 基于单元整体视角的复习课教学探索
教学实践 | 基于单元整体视角的复习课教学探索
-
教学实践 | 基于“学材再建构"的初中数学概念教学实践研究
教学实践 | 基于“学材再建构"的初中数学概念教学实践研究
-

教学实践 | 基于“问题意识"培养的初中数学教学研究
教学实践 | 基于“问题意识"培养的初中数学教学研究
-
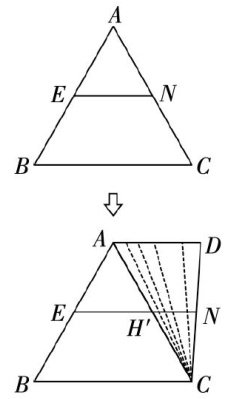
教学实践 | 关注探索过程 促进深度学习 发展核心素养
教学实践 | 关注探索过程 促进深度学习 发展核心素养
-
教学实践 | 基于“三会"能力发展的初中数学教学实践与思考
教学实践 | 基于“三会"能力发展的初中数学教学实践与思考
-

教学实践 | 深度学习视角下初中数学有效课堂教学的实施
教学实践 | 深度学习视角下初中数学有效课堂教学的实施
-

教学实践 | “一题一课"教学模式助力中考复习
教学实践 | “一题一课"教学模式助力中考复习
-
教学实践 | 以生为主 问题引领 自主建构
教学实践 | 以生为主 问题引领 自主建构
-
教研在线 | 价值、内涵与策略: 初中数学跨学科教学的探索
教研在线 | 价值、内涵与策略: 初中数学跨学科教学的探索
-

教研在线 | 核心素养视域下初中数学教学设计研究
教研在线 | 核心素养视域下初中数学教学设计研究
-
教研在线 | 基于“四能"培养的初中数学跨学科学习
教研在线 | 基于“四能"培养的初中数学跨学科学习
-
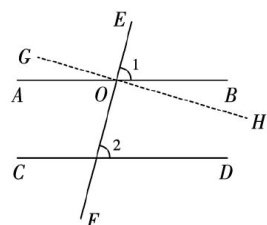
教研在线 | 以初中数学课堂作业优化支撑课后优质服务
教研在线 | 以初中数学课堂作业优化支撑课后优质服务
-

教研在线 | 单元整体视域下的初中数学复习教学研究
教研在线 | 单元整体视域下的初中数学复习教学研究
-

问题探索 | 用代数思维赋能几何结构化教学
问题探索 | 用代数思维赋能几何结构化教学
-

问题探索 | 知识结构解读,教学模块思考
问题探索 | 知识结构解读,教学模块思考
-
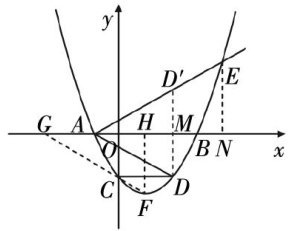
问题探索 | 核心素养视域下的初中数学讲评课教学策略
问题探索 | 核心素养视域下的初中数学讲评课教学策略
-

问题探索 | 关于数学建模思想的应用探究教学
问题探索 | 关于数学建模思想的应用探究教学
-

问题探索 | 瓜豆原理之直线轨迹模型教学探究
问题探索 | 瓜豆原理之直线轨迹模型教学探究
-

问题探索 | 知识整合定理构建,分层引导教学探索
问题探索 | 知识整合定理构建,分层引导教学探索
-
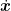
问题探索 | 引例解析知识生成 过程探究教学设计
问题探索 | 引例解析知识生成 过程探究教学设计
-
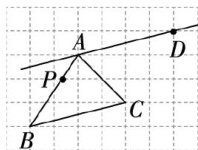
问题探索 | 拨开云雾见天明,网格作图基本方法初探
问题探索 | 拨开云雾见天明,网格作图基本方法初探
-
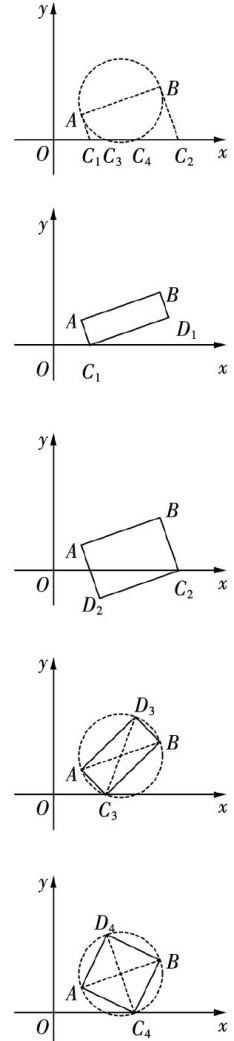
试题研究 | 二次函数背景下的矩形存在性问题教学探究
试题研究 | 二次函数背景下的矩形存在性问题教学探究
-

试题研究 | 展现学生多彩思维
试题研究 | 展现学生多彩思维























 登录
登录