目录
快速导航-
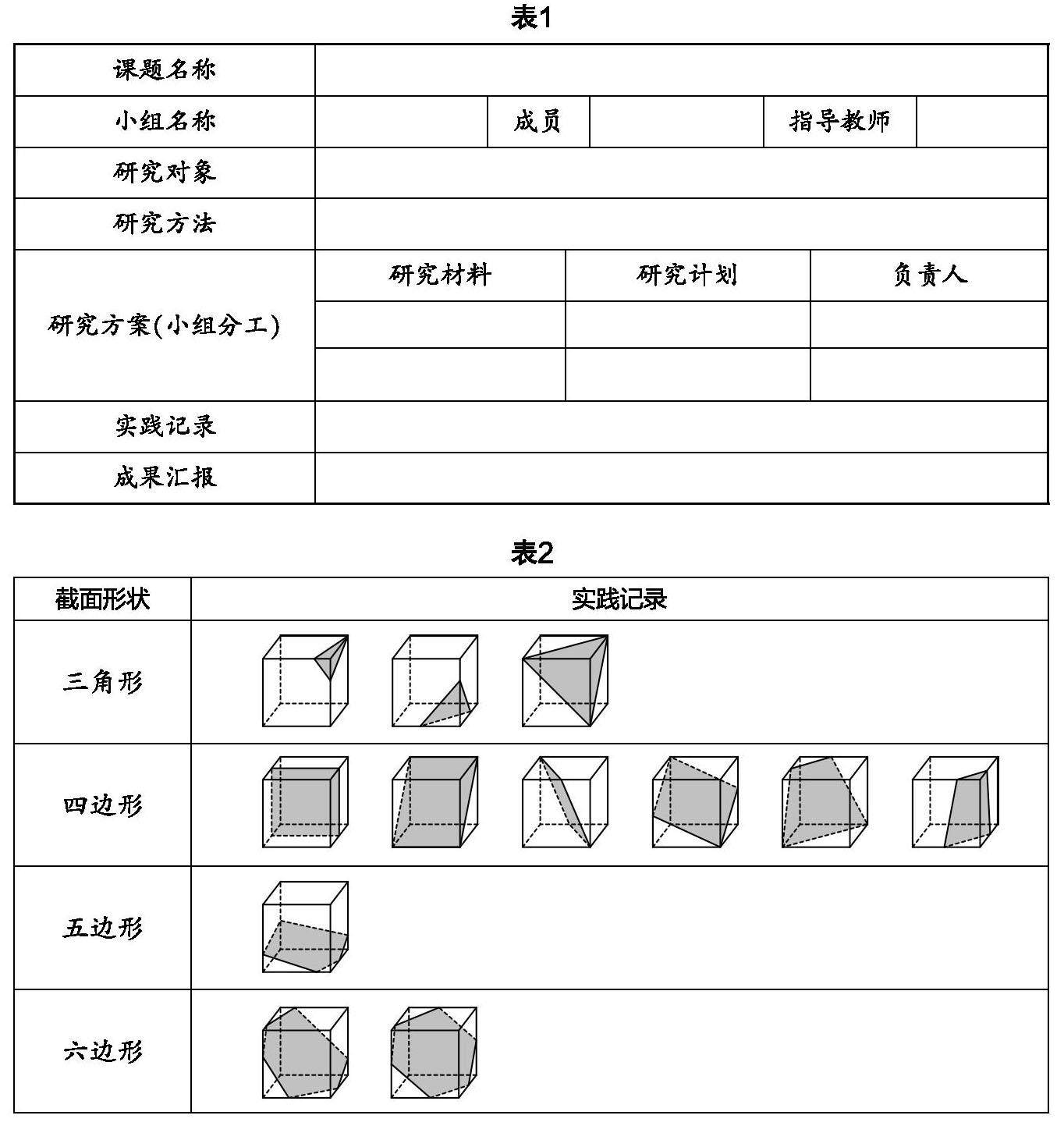
课程教材教法 | 基于“综合与实践”项目式学习的数学教学设计探究
课程教材教法 | 基于“综合与实践”项目式学习的数学教学设计探究
-
课程教材教法 | 基于“探究规律”的综合实践活动课设计与实施研究
课程教材教法 | 基于“探究规律”的综合实践活动课设计与实施研究
-
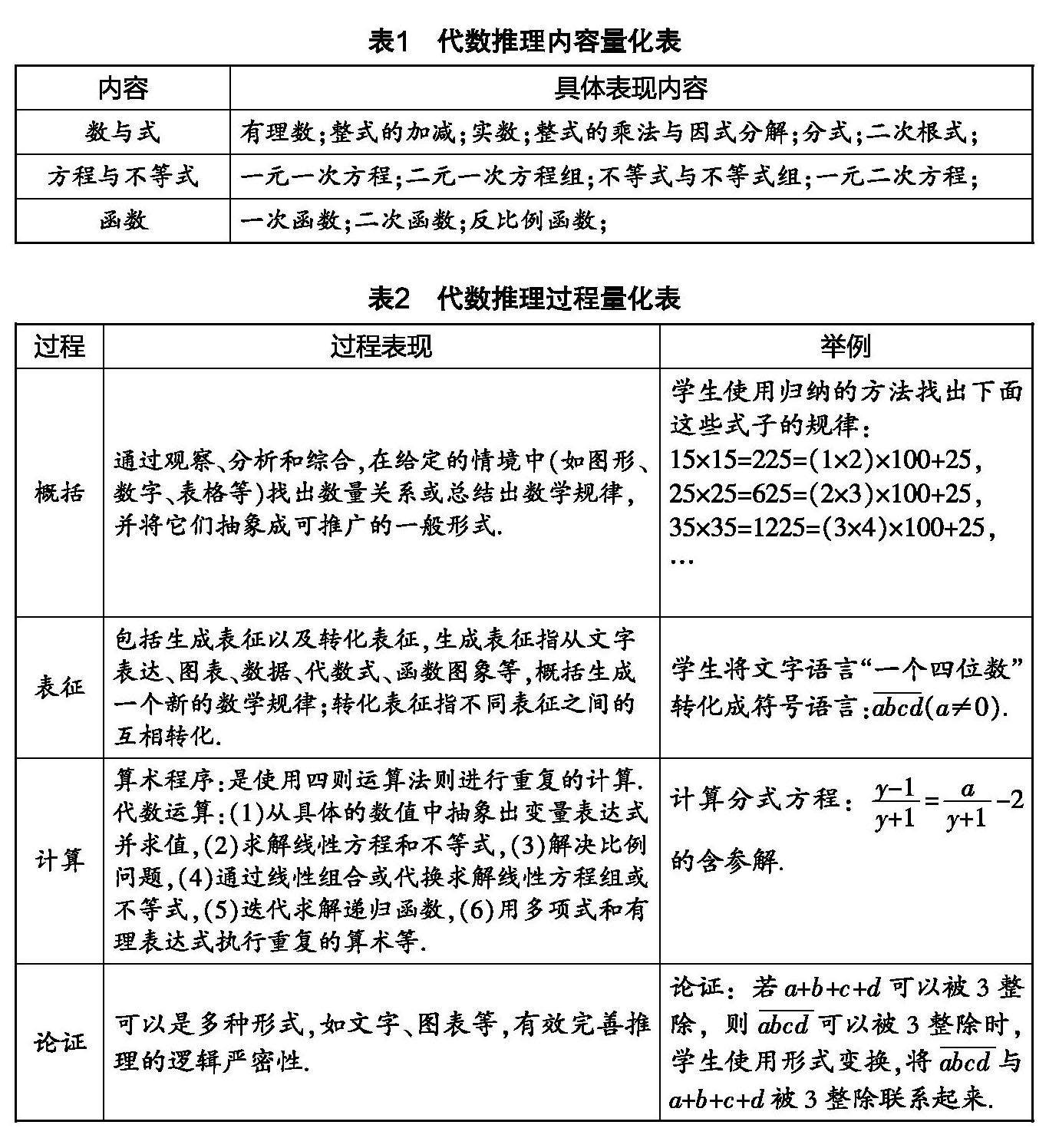
课程教材教法 | 中考数学“代数推理类”试题的分析与思考
课程教材教法 | 中考数学“代数推理类”试题的分析与思考
-
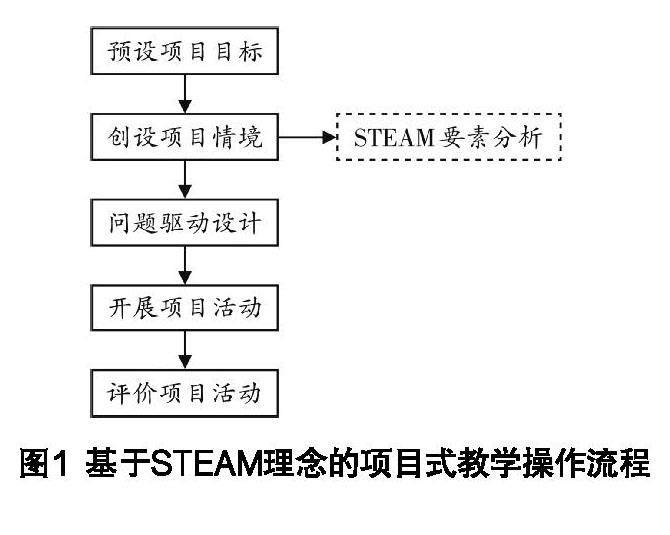
课程教材教法 | 基于STEAM教育理念的项目式学习的设计与实施
课程教材教法 | 基于STEAM教育理念的项目式学习的设计与实施
-
教学实践 | 如切如磋 如琢如磨
教学实践 | 如切如磋 如琢如磨
-

教学实践 | 初中数学“生态结构化”单元起始课教学的思考与实践
教学实践 | 初中数学“生态结构化”单元起始课教学的思考与实践
-
教学实践 | 核心素养指向下的初中数学整体化教学
教学实践 | 核心素养指向下的初中数学整体化教学
-
教学实践 | 基于“三个理解”的“一定是直角三角形吗”教学设计及思考
教学实践 | 基于“三个理解”的“一定是直角三角形吗”教学设计及思考
-
教学实践 | 自主展评模式下初中数学专题教学的实践研究
教学实践 | 自主展评模式下初中数学专题教学的实践研究
-
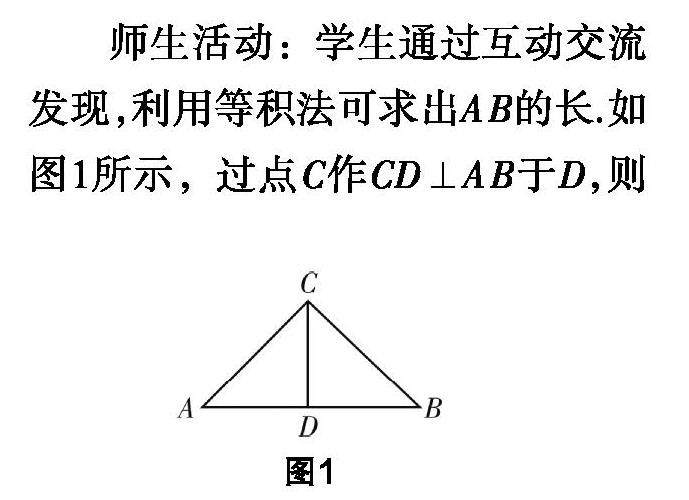
教学实践 | 数学实验:基本活动经验培养的最佳方式
教学实践 | 数学实验:基本活动经验培养的最佳方式
-

教学实践 | 以生为本 关注过程 提升素养
教学实践 | 以生为本 关注过程 提升素养
-

教学实践 | 巧借深层拓展研究 发展学生综合能力
教学实践 | 巧借深层拓展研究 发展学生综合能力
-

教学实践 | 变式中层进 层进中拓展
教学实践 | 变式中层进 层进中拓展
-

教学实践 | 聚焦“激励、唤醒、鼓舞”,揭露知识本质
教学实践 | 聚焦“激励、唤醒、鼓舞”,揭露知识本质
-

教学实践 | 关注元认知训练,让深度学习真实发生
教学实践 | 关注元认知训练,让深度学习真实发生
-
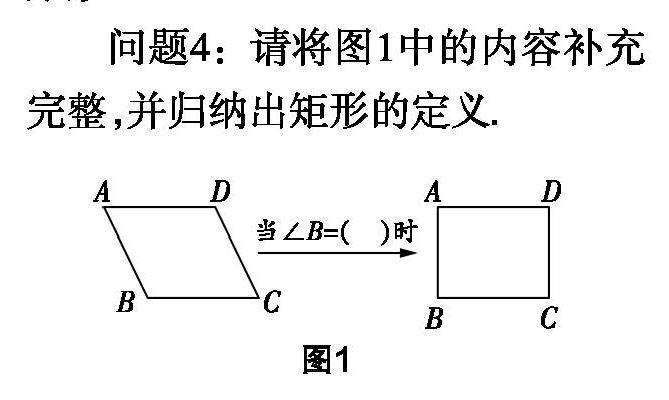
教学实践 | 基于问题解决的初中数学单元教学设计研究
教学实践 | 基于问题解决的初中数学单元教学设计研究
-

教学实践 | 智育数学课堂 发展核心素养
教学实践 | 智育数学课堂 发展核心素养
-

教学实践 | 跳出圈子思维 培养模型观念
教学实践 | 跳出圈子思维 培养模型观念
-

教学实践 | 浅谈学情分析在课堂教学设计中的实践与意义
教学实践 | 浅谈学情分析在课堂教学设计中的实践与意义
-
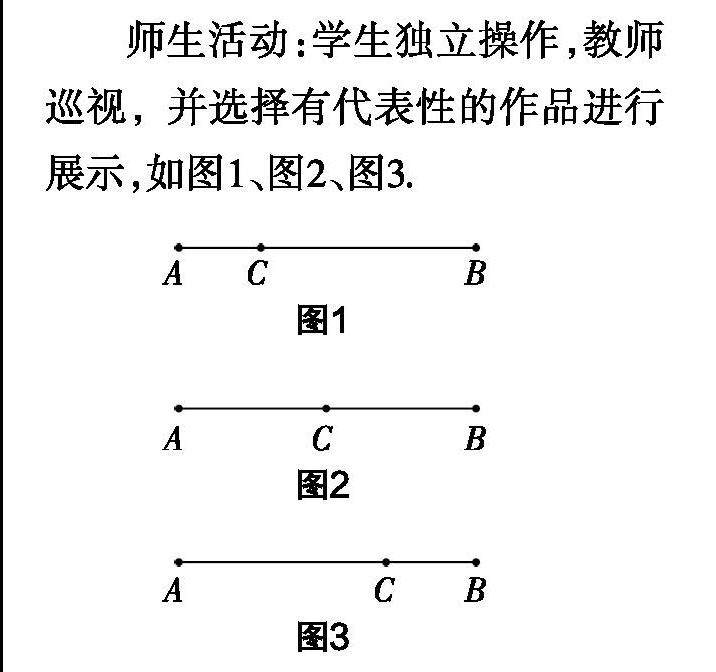
教学实践 | 问题驱动视角下初中数学概念教学
教学实践 | 问题驱动视角下初中数学概念教学
-

教学实践 | 大单元视域下初中数学问题链教学实践的研究
教学实践 | 大单元视域下初中数学问题链教学实践的研究
-

教学实践 | 数学文化视角下基于“大概念”的勾股定理教学
教学实践 | 数学文化视角下基于“大概念”的勾股定理教学
-
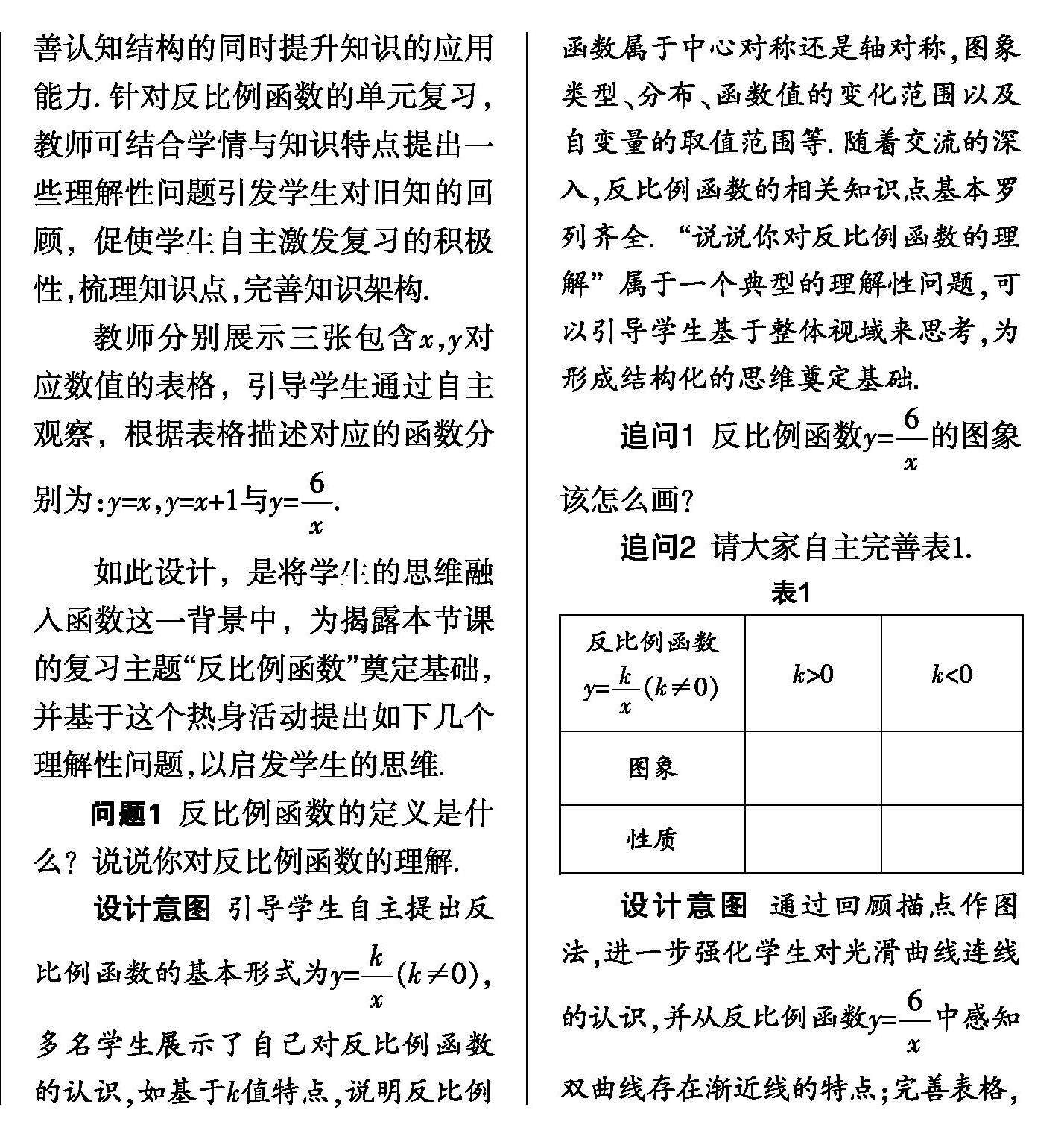
教学实践 | 立足于问题驱动 优化单元复习教学
教学实践 | 立足于问题驱动 优化单元复习教学
-
教研在线 | 指向初中生数学抽象素养发展的情境教学实践研究
教研在线 | 指向初中生数学抽象素养发展的情境教学实践研究
-
教研在线 | 立足“差异现实”,实施初中数学分层教学
教研在线 | 立足“差异现实”,实施初中数学分层教学
-

教研在线 | 渗透“模型思想”的初中数学教学研究
教研在线 | 渗透“模型思想”的初中数学教学研究
-
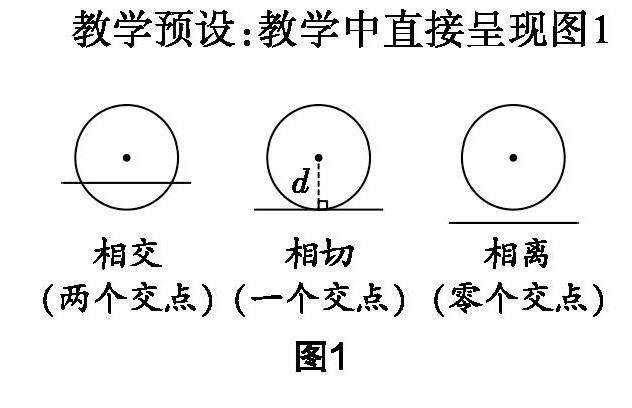
教研在线 | 关于“切线的判定”的复习教学探究与思考
教研在线 | 关于“切线的判定”的复习教学探究与思考
-
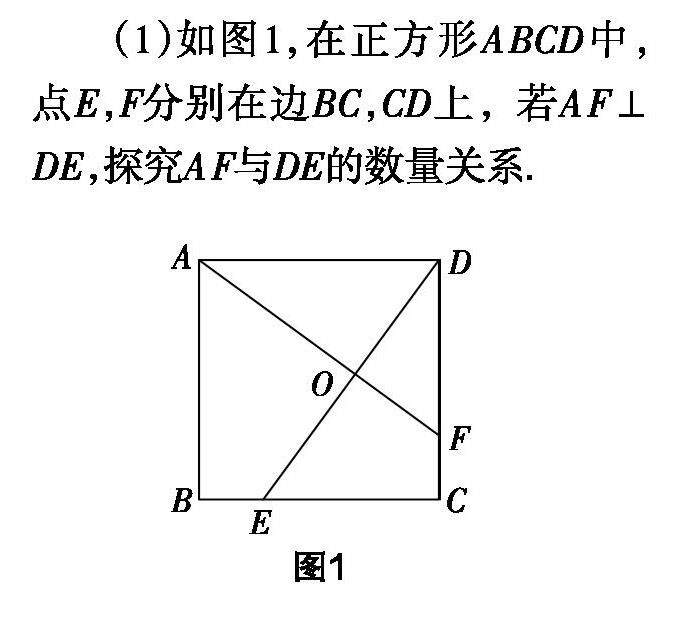
教学技巧 | 重视学法指导 提升学习能力
教学技巧 | 重视学法指导 提升学习能力
-

教学技巧 | 关注整体 合理类比 提升素养
教学技巧 | 关注整体 合理类比 提升素养
-
教学技巧 | 聚焦深度学习 发展核心素养
教学技巧 | 聚焦深度学习 发展核心素养
-
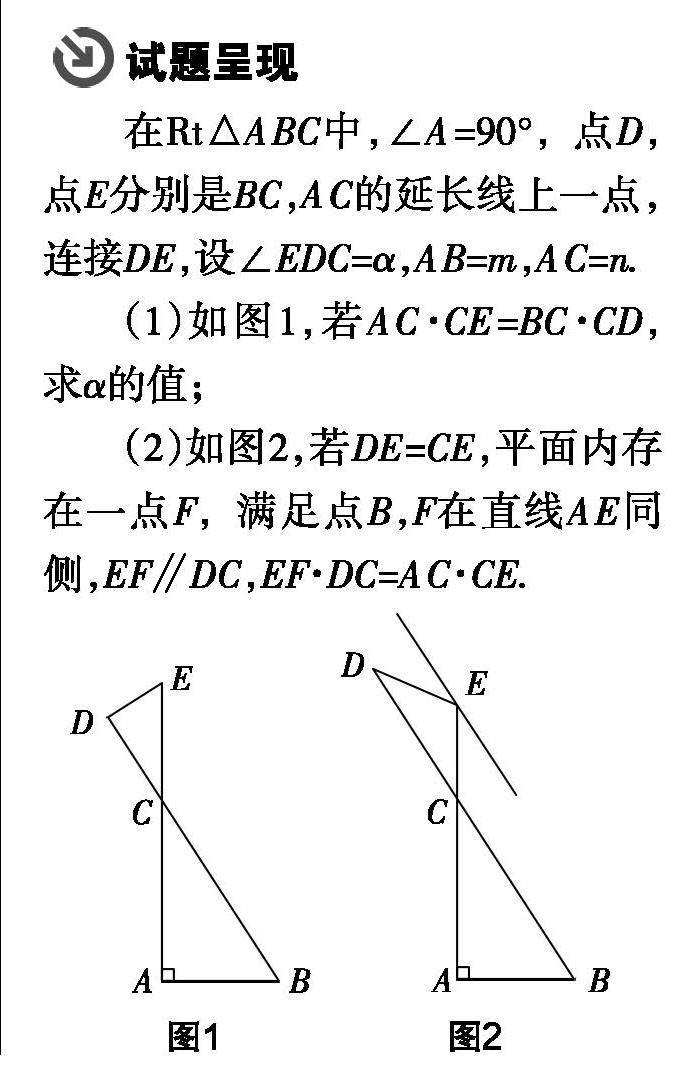
试题研究 | 抓住问题根源 回归数学本质
试题研究 | 抓住问题根源 回归数学本质
-
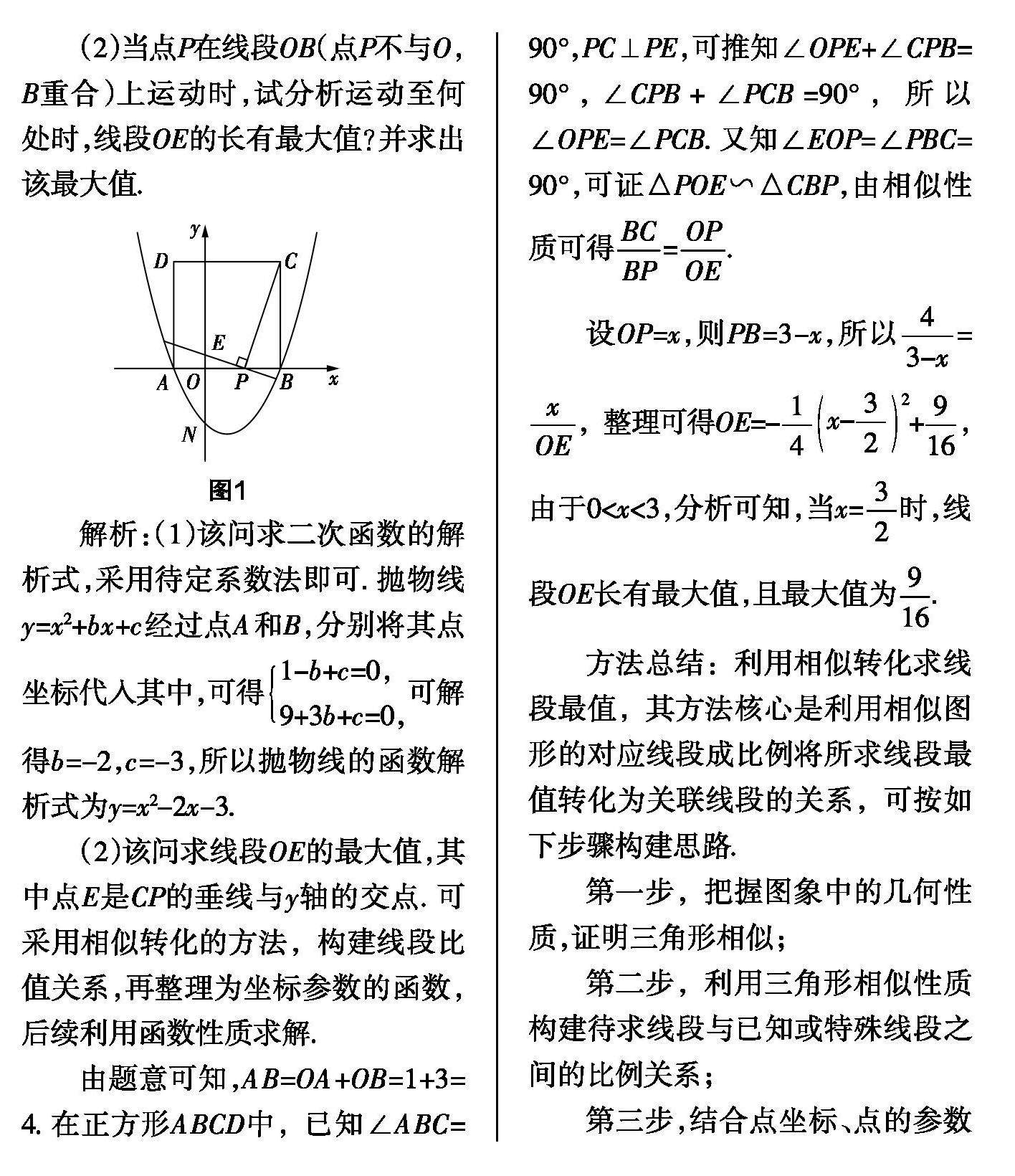
试题研究 | 二次函数中的线段最值问题转化法的探究
试题研究 | 二次函数中的线段最值问题转化法的探究























 登录
登录